BAND GAPS AND EXCITATIONS WITHOUT ALL THE FUSS – EIGENVECTOR CONTINUATION FOR SPECTRAL FUNCTIONS

Work package:
Leveraging the opto-electronic properties of quantum materials for device design requires a careful understanding of how spectral functions respond to changes in external parameters, like pressure of doping. From a theoretical modelling perspective, this calls for mapping out correlation functions across large subspaces of a material’s phase diagram. The traditional approach relies on repeatedly solving the electronic structure problem for dense grids sampling the parameter range of interest. Needless to say, this quickly becomes extremely computationally intensive, even prohibitive when sophisticated approximations are needed. 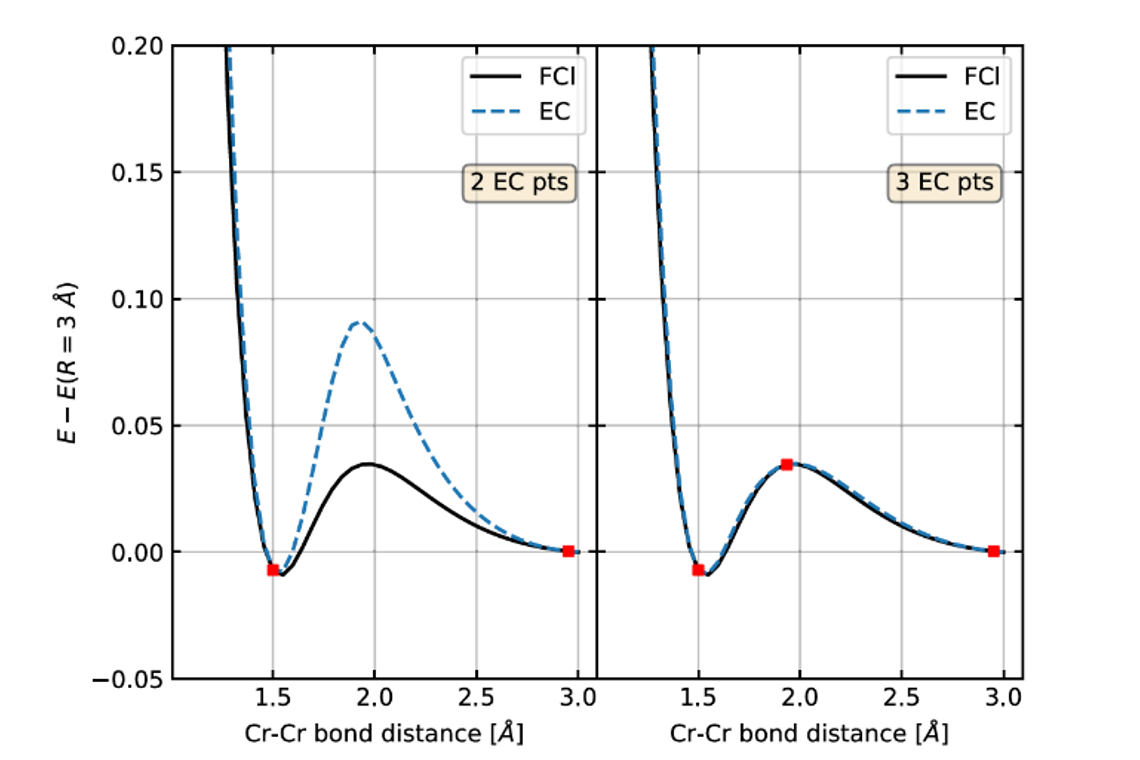Recently, a new strategy has arisen to possibly avoid this computational overhead: the Eigenvector Continuation Ansatz [1-3]. The idea is identifying a small number of representative points in phase space and using their solutions as a linear expansion basis to reconstruct the properties of interest everywhere else in the phase diagram. Remarkably, this has been shown to result in extremely-compact representations of ground state energies in lattice models and molecular systems: enabling the expansion of dissociation potential energy surfaces with as few as 3-5 representatives [2], and even allowing the simulation of non-adiabatic dynamics in H28 chains with as little as 22 points [3]. In this project, we will explore the application of Eigenvector Continuation beyond ground state energies, namely to the prediction of spectral functions. We will focus on many-body perturbation theory approximations for the one-body Green’s function, taking advantage of effective Hamiltonian formulations to directly apply the Eigenvector Continuation idea to the evaluation of spectra.