Novel subradiant states in 1D atomic chains

Work package:
Cooperative effects in an N-emitter sample lead to very specific radiative features known as super- and subradiance, i.e. the enhancement and inhibition, respectively, of light spontaneous emission with respect to the N-independent-emitter case. While superradiance has been extensively studied since Dicke’s seminal work [1], subradiance of a large ensemble was observed only very recently in cold atom clouds [2,3] and metamaterial arrays [4]. Comprehensive theoretical tools to fully describe subradiance are still elusive [5–8] due to the complicated long-range interactions and many-body features of the atomic ensembles [9–11]. It was, however, proved that subradiant suppression of radiative decay has potential promising applications in quantum memories [12,13], excitation transfer [14–16], and topological photonics [17,18]. 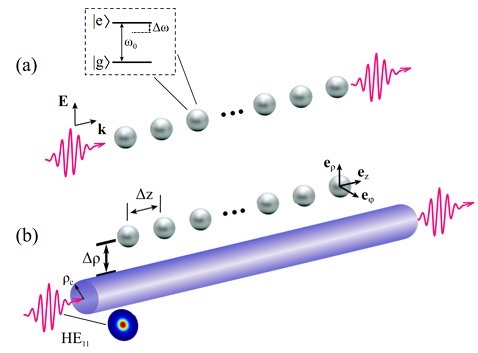A one-dimensional (1D) chain of equally spaced two-level atoms is the paradigmatic situation which offers the simplest geometry to gain insight in the collective decay mechanisms. Recently, one-dimensional (1D) emitter arrays with subwavelength separations were found to have subradiant states with decay rates scaling as N−3 [19], but examples of rates scaling with N−α with α > 3 were also soon identified [20]. The close relationship between subradiance and the band flatness of collectively shared atomic excitations is a crucial component of the collective dipole-dipole interaction [21]. The implementation of such chains coupled to nanofibers [22] (see Figure), 1D waveguides [23], and the full vacuum electromagnetic field in 3D free space [24] has attracted considerable attention. In addition to super- and subradiance phenomena these systems exhibit further interesting properties and applications such as atomic mirrors [25], photon Fock state synthesis [26], enhancement of cooperativity [27], and applications in quantum computation [28]. The present project aims at going beyond previous theoretical works by investigating the radiance properties of 1D atomic arrays whose step varies in space. Once the constant step constraint is relaxed, many different novel configurations may be considered : the slow monotonic change of the distance between two successive neighbours ; the abrupt jump from a step value to another – which can be seen as the junction of two (or more) atomic chains with different constant steps ; the periodic modulation of the step of the array ; etc. Our goal is to explore the existence and form of subradiant states in such new arrangements, as well as the influence of the geometric features – rate of change of the step, period of modulation, … – on these states. It will also be interesting to determine how photonic excitations propagate in such structures. To be more specific, we shall focus on the case when the atomic chain interacts with a 1D waveguide, such as an optical nanofibre. Due to the complexity of this (typically many-body) problem, we shall resort to numerical simulations of the master equation governing the dynamics of atoms interacting with the electromagnetic field, and restrict ourselves to cases of moderate excitation numbers – typically one or two. When possible, e.g. when step is very slightly and smoothly varied, numerical results will be complemented by analytical perturbative treatment, which will help understanding how radiance properties are affected by the step variations. Despite the fundamental character of the planned research, we expect that the great wealth of emerging behaviours in these novel configurations will lead to promising new schemes for quantum devices, such as quantum switches or mirrors.